Calculadora de Juros Compostos
| Mês | Valor Investido | Juros do Mês | Valor com Juros |
|---|
Calculadora de Juros Compostos
A calculadora de juros compostos é uma ferramenta poderosa para planejar seus investimentos e entender como diferentes valores, taxas e prazos afetam o crescimento do seu patrimônio.
Como usar a Calculadora:
• Valor Inicial: Comece inserindo o valor inicial que você deseja investir. Esse é o montante principal que será utilizado para calcular os juros compostos.
Exemplo: Se você tem R$ 1.000,00 para investir, insira esse valor no campo correspondente.
• Valor Mensal: Insira o valor que pretende adicionar ao investimento todos os meses. Esse campo é importante, porque os aportes mensais aumentam o montante principal e, consequentemente, os juros compostos sobre ele.
Exemplo: Se você pode investir R$ 200,00 por mês, insira esse valor.
• Taxa de Juros: Informe a taxa de juros do seu investimento e sem seguida defina se a taxa será anual ou mensal.
Exemplo: Se o seu investimento oferece uma taxa de 10% ao ano, insira “10” no campo da taxa de juros e depois marque a opção “anual”.
• Período: Informe o prazo do seu investimento e em seguida defina se será em meses ou anos.
Exemplo: Se você deseja investir por 2 anos, insira “2” no campo correspondente e depois marque a opção “anos”.
• Calcular: Clique no botão “Calcular” para gerar os resultados. A calculadora mostrará o crescimento do seu investimento ao longo do tempo, com base nos dados que você inseriu.
Analisando os Resultados:
A calculadora de juros compostos oferece três formatos principais de resultado: o resultado simples, a tabela detalhada e o gráfico de linhas. Entender como interpretar cada um deles é essencial para aproveitar ao máximo a ferramenta.
Resultado Simples:
Para o resultado simples, a calculadora irá exibir três informações importantes. São elas:
• Valor Investido: O valor inicial mais os aportes mensais, sem o acréscimo dos juros.
• Valor dos Juros: O valor correspondente somente aos juros no período.
• Valor Total com Juros: O valor total do investimento, que é o valor investido mais os juros acumulados.

Tabela Detalhada:
A tabela irá mostrar detalhadamente, mês a mês, como o seu investimento crescerá. Ela inclui:
• Valor Investido: O valor inicial investido atualizado mês a mês com os aportes.
• Juros do Mês: O valor mensal dos juros, correspondente ao valor investido.
• Valor com Juros: O valor total somado aos juros.
A tabela é útil para observar de forma detalhada como os juros compostos trabalham ao longo do tempo. Ela permite ver como pequenas quantias de juros se acumulam e aumentam o valor total do investimento. Esse detalhamento ajuda a entender o impacto de cada aporte mensal e dos juros mensais no investimento.
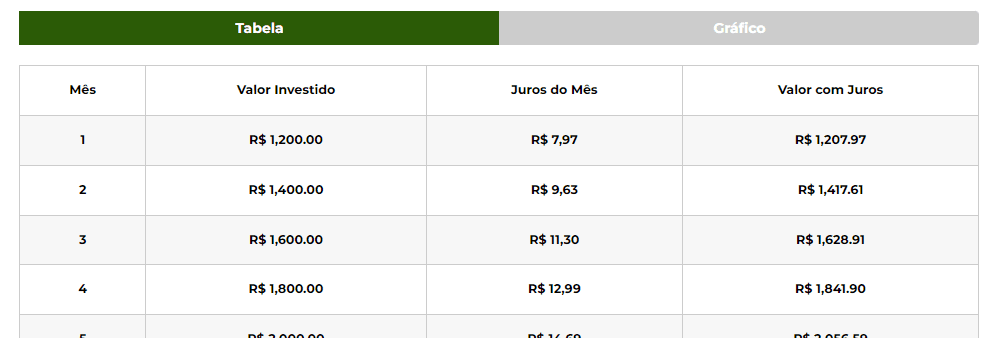
Gráfico de Resultados:
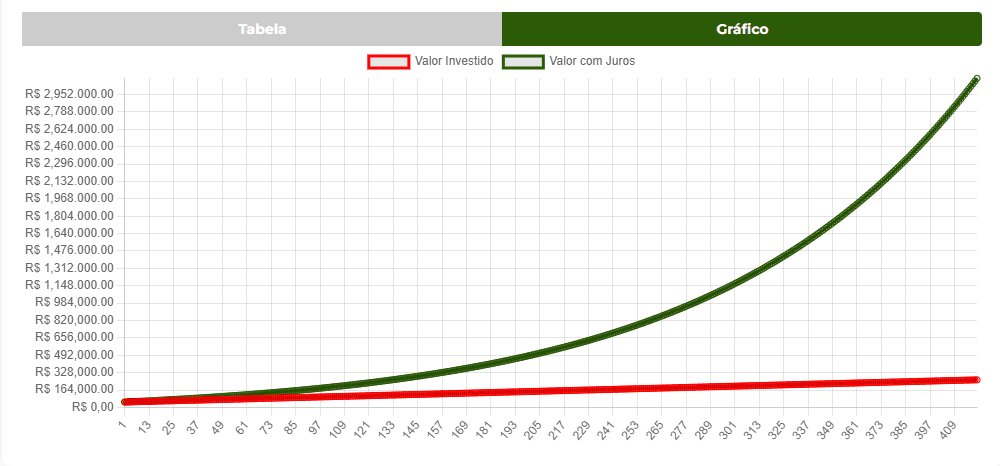
O gráfico de linhas permite uma visualização clara e direta do crescimento do seu investimento ao longo do tempo. Ele apresenta dois eixos principais:
• Eixo Vertical: Representa o valor em dinheiro.
• Eixo Horizontal: Representa o tempo em meses.
Elementos visuais:
• Linha Vermelha: Representa o valor investido sem considerar os juros.
• Linha Verde: Mostra o valor investido mais os juros.
• Tooltip: Uma pequena caixa de texto que mostra os resultados do gráfico.
O gráfico é ideal para visualizar o crescimento exponencial proporcionado pelos juros compostos. Ele ajuda a entender como o investimento se desenvolve ao longo do tempo e a identificar o ponto em que os juros compostos começam a ter um impacto significativo no montante total.
O que são Juros Compostos
Primeiro é preciso entender que juros podem ser definidos como o preço que se paga por utilizar o dinheiro de terceiros, em outras palavras, é uma espécie de aluguel do dinheiro, onde aquele que pega emprestado paga os juros, e aquele que empresta, os recebe.
Dessa forma, o conceito de juros compostos é um dos mais poderosos no mundo de finanças e investimentos, justamente porque eles têm a capacidade de transformar investimentos pequenos em grandes fortunas ao longo do tempo.
E isso acontece devido ao fato de não serem calculados apenas sobre o valor principal de um investimento ou empréstimo, mas também sobre os juros que já foram acumulados em períodos anteriores. Por isso o nome de “juros sobre juros”.
Além disso, os juros compostos são de natureza exponencial, ou seja, quanto mais tempo um investimento estiver aplicado, maior será a diferença entre o valor inicial investido e o montante final resgatado no vencimento da aplicação (valor inicial acrescido de juros).
Como Funcionam os Juros Compostos?
Para entender melhor o funcionamento, basta pensar que a cada período o valor dos juros é adicionado ao montante principal, fazendo com o próximo período tenha juros ainda maiores.
Por exemplo:
• Imagine que você invista R$ 5.000,00 a uma taxa de 1% ao mês, em um regime de juros compostos.
• Após o primeiro mês, você terá R$ 5.050,00 (Sendo R$ 5.000,00 + 1%)
• No segundo mês, o 1% será aplicado sobre R$ 5.050,00, resultando em um total de R$ 5.100,50.
• No terceiro mês, será aplicado sobre R$ 5.100,50, resultando em R$ 5.151,50.
• No quarto mês, aplicado sobre R$ 5.151,50, resultando em R$ 5.203,01.
E esse processo é contínuo, a cada período o montante cresce um pouco mais rápido do que no período anterior. Por isso, quanto mais longo for o prazo em que o dinheiro está investido, maior o efeito dos juros compostos sobre o investimento.
Fórmula dos Juros Compostos
A fórmula para calcular os juros compostos é a seguinte:
Cada uma dessas letras tem um significado para a matemática financeira:
• M = É o montante total ao final da aplicação (capital inicial + juros).
• C = Capital é o primeiro valor a ser investido. Esse valor também é chamado de principal.
• i = Representa a taxa de juros, que pode ser mensal, bimestral, trimestral, quadrimestral, semestral ou anual, e deve ser expressa em decimal. Por exemplo, 10% = 0,10.
• t = É o tempo em que o capital ficará investido, e deve estar sempre na mesma unidade de medida da taxa de juros. Ou seja, se a taxa estiver em meses o tempo deverá ser em meses, se estiver em anos, o tempo deverá ser em anos.
Como Calcular os Juros Compostos
Para entender como calcular uma aplicação a juros compostos sem a calculadora, devemos utilizar a fórmula. Alguns exemplos de como calcular são:
• Um investimento de R$ 5.000,00, a uma taxa de 10% ao ano, com período de 3 anos:
M = C x (1+i) ^t
M = 5.000 x (1+0,10) ^3
M = 5.000 x (1,10) ^3
M = 5.000 x 1,331
M = 6.655
O montante final desse investimento será de R$ 6.655,00.
• Um investimento de R$ 3.000,00, a uma taxa de 1% ao mês, por um período de 2 anos.
M = C x (1+i) ^t
M = 3.000 x (1+0,01) ^24
• Lembre que sempre deve utilizar a mesma unidade de medida entre taxa e tempo, por isso 2 anos, se tornam 24 meses.
M = 3.000 x (1,01)^24
M = 3.000 x 1,2697
M = 3.807
O montante final desse investimento seria de R$ 3.809,10
• Um investimento de R$ 10.000,00, a uma taxa de 8% ao ano, por um período de 30 meses.
• Para deixar a taxa de juros na mesma unidade de medida do período, vamos precisar utilizar outra fórmula, que parece assustadora, mas não é.
A fórmula é essa: Iq = [(1 + It)^q/t - 1] x 100. Mas calma que vai ficar fácil de entender e aplicar.
Iq = Significa a taxa de juros no período que você quer, basta pensar em “I+quero”.
It = Significa a taxa de juros no período que você tem, basta pensar em “I+tenho”.
q = período que você quer, “q de quero”.
t = período que você tem, “t de tenho”
• Antes de calcular os juros compostos, você precisará descobrir a taxa de juros equivalente em meses. Para isso, é só colocar os valores na fórmula:
Iq = [(1 + It) ^q/t - 1] x 100
Iq = [(1 + 0,08) ^1/12 - 1] x 100
Iq = [(1,08) ^0,0833 - 1] x 100
Iq = [1,0064 - 1] x 100
Iq = [0,0064] x 100
Iq = 0,64
• Dessa forma, é possível saber que o investimento rende 0,64% ao mês e aplicá-lo corretamente na fórmula de juros compostos. Não esquecendo de usá-lo em sua forma decimal, que é 0,0064.
M = C x (1+i) ^t
M = 10.000 x (1+0,0064) ^30
M = 10.000 x (1,0064) ^30
M = 10.000 x 1,212
M = 12.120
Dessa forma o montante final para esse investimento seria de aproximadamente R$ 12.120,00.
Essas fórmulas podem parecer intimidadoras à primeira vista, mas são simples de entender e fundamentais para compreender como os juros compostos funcionam, e como eles podem de verdade impactar seus investimentos.
Onde os Juros Compostos São Utilizados
Os juros compostos são utilizados em diversas áreas do setor financeiro, desde investimentos até financiamentos e dívidas. Alguns exemplos onde são utilizados, são:
• Investimentos em Renda Fixa: Produtos como CDBs, LCIs e Tesouro Direto utilizam juros compostos para calcular seu rendimento.
• Cartões de Crédito: O saldo devedor de um cartão de crédito pode crescer absurdamente rápido se não for pago em dia, devido aos juros compostos.
• Empréstimos e Financiamentos: Os juros compostos são aplicados sobre o saldo, o que pode aumentar ainda mais o valor total a ser pago no longo prazo. Por isso é essencial entender a taxa de juros e o período, antes de contrair esses produtos.
• Poupança: Embora a taxa de juros da poupança seja baixa, os juros compostos ainda são aplicados sobre o saldo acumulado.
Diferença entre Juros Simples e Juros Compostos
A principal diferença entre juros simples e juros compostos está na forma como os juros são calculados:
• Juros Simples: São calculados somente sobre o valor principal inicial, sem considerar os juros acumulados ao longo do tempo.
• Juros Compostos: São calculados sobre o valor principal acrescido dos juros acumulados de períodos anteriores.
Isso faz com que a diferença no resultado final seja muito grande, tanto no caso dos investimentos, quanto de financiamentos e dívidas.
Por exemplo:
• Se você investir R$ 10.000,00, a uma taxa de 10% ao ano, por um período de 30 anos, em regime de juros simples.
O montante final será de R$ 40.000,00
• Se você investir R$ 10.000,00, a uma taxa de 10% ao ano, por um período de 30 anos, em regime de juros compostos.
O montante final será de R$ 174.494,02
Uma diferença de R$ 134.494,02 entre um regime de juros e o outro.
* Lembrando que considerei só o valor inicial, sem aportes mensais. Considerando aportes mensais, essa diferença seria muito maior.
Você pode pensar agora “ah, mas 30 anos é muito tempo, por isso essa diferença grande”, e você tem razão, os juros compostos têm mais poder nos investimentos quando aliados a um tempo longo.
Mas isso também é verdadeiro para os financiamentos. Quando alguém contrai um financiamento de 360 meses, ou 30 anos, geralmente está em regime de juros compostos, por isso é importante saber a diferença entre eles.
Porque sabendo que o financiamento é em regime de juros compostos, você sabe que quanto mais tempo demorar para pagar, mais caro ele ficará.
O Poder dos Juros Compostos
Para fazer um breve resumo e ficar ainda mais claro os pontos citados, pode-se afirmar que os juros compostos permitem que o dinheiro “trabalhe” mais para você, acumulando rendimentos sobre rendimentos, de forma contínua.
Quanto mais tempo o dinheiro permanecer investido, maior será o impacto dos juros compostos. E isso serve “para o bem e para o mal”, tanto para investimentos quanto para dívidas.
Levando isso em consideração, a melhor hora para começar a investir é agora! Porque quanto mais cedo seu dinheiro começar a “trabalhar”, mais tempo ele terá para aproveitar ao máximo o poder dos juros compostos.
Conclusão
Compreender os juros compostos e saber como utilizá-los a seu favor é essencial para alcançar a liberdade financeira. Para te ajudar com isso, nós disponibilizamos uma calculadora de juros compostos. Fique à vontade, para planejar seus investimentos, analisar os resultados com atenção e entender como potencializar ainda mais sua estratégia de investimento.
Agora que você já sabe de tudo isso, não fique com esse conhecimento só para você. Compartilhe esse artigo e nossa calculadora com pessoas que você acredita que querem ou precisam dessas informações.
Juntos nós podemos fazer um mundo investidor.


