A Teoria de Markowitz é um dos pilares mais influentes da moderna análise de investimentos. Ao introduzir uma lógica estruturada para equilibrar risco e retorno, ela transformou a maneira como profissionais constroem portfólios e avaliam a eficiência das carteiras. No mercado brasileiro, marcado por ciclos econômicos intensos, volatilidade setorial e oscilações de juros, compreender esse modelo significa enxergar a carteira de investimentos com um rigor matemático capaz de orientar decisões mais seguras e consistentes.
Neste artigo, você entenderá em profundidade o que é a Teoria de Markowitz, como funciona seu cálculo, por que a fronteira eficiente representa uma virada de chave na análise de risco e como esse conceito se aplica ao cotidiano financeiro. O conteúdo foi estruturado para ser didático e aplicado, criando uma ponte natural com o universo da análise profissional.
Quem foi Harry Markowitz e por que sua teoria mudou a história dos investimentos
A origem da Teoria Moderna do Portfólio remonta ao trabalho do economista norte-americano Harry Max Markowitz, nascido em 1927, em Chicago. Em um período em que o mercado financeiro era dominado por análises isoladas de títulos e ações, Markowitz identificou uma lacuna metodológica que dificultava a avaliação real do risco agregado das carteiras.

O modelo mais utilizado até então era o de John Burr Williams, baseado no Valor Presente dos Fluxos de Caixa. Embora relevante, essa abordagem não contemplava as interações estatísticas entre ativos. Para Markowitz, analisar retornos de forma isolada tornava impossível compreender o risco conjunto e a dinâmica de uma carteira diversificada. Era necessário olhar para o portfólio como um sistema interdependente, e não como um conjunto de peças separadas.
Em 1952, sua pesquisa foi publicada no Journal of Finance, introduzindo formalmente o modelo que viria a mudar a forma como investidores profissionais distribuem capital entre diferentes ativos. Décadas depois, o impacto de sua contribuição foi reconhecido com dois prêmios relevantes: o John Von Neumann Theory Prize em 1989 e o Nobel de Ciências Econômicas em 1990.
O que é a Teoria de Markowitz
A Teoria de Markowitz é um modelo matemático que busca identificar a melhor relação entre risco e retorno em uma carteira de investimentos. Seu objetivo central é simples e profundo: encontrar a combinação de ativos capaz de oferecer o maior retorno possível para um determinado nível de risco, ou reduzir o risco ao máximo para um retorno desejado.
Essa lógica mudou a forma de investir porque desloca a atenção do desempenho individual de cada ativo para o comportamento coletivo da carteira. A correlação entre os ativos, e não apenas a performance isolada, se torna o elemento-chave da eficiência.
A teoria considera três elementos fundamentais:
- Retornos esperados
- Variância e desvio padrão como medidas de risco
- Correlação entre os ativos
Quando esses fatores são organizados matematicamente, surge a curva conhecida como Fronteira Eficiente, que representa o limite máximo de eficiência possível em uma carteira. Antes de chegar a esse ponto, é essencial compreender como se calcula o retorno e o risco de um portfólio.
Como funciona a Teoria de Markowitz na prática
A lógica da teoria é progressiva. Primeiro calcula-se o retorno da carteira. Depois o risco. Por fim, avalia-se a relação entre ambos, buscando combinações melhores na comparação entre diferentes portfólios.
Cálculo do retorno de uma carteira
O retorno esperado de um portfólio é obtido através da média ponderada dos retornos individuais dos ativos. A fórmula é simples, e embora pareça matemática pura, ela traduz exatamente a proporção em que cada ativo contribui para o resultado final.
Fórmula:
Rp = Wa x Ra + Wb x Rb
Em que:
- Rp representa o retorno da carteira
- Wa e Wb representam os pesos dos ativos
- Ra e Rb representam os retornos individuais
Como exemplo, imagine a seguinte carteira fictícia:
- Ativo A, peso de 30%, retorno de 14%
- Ativo B, peso de 40%, retorno de 9%
- Ativo C, peso de 15%, retorno de 11%
- Ativo D, peso de 15%, retorno de 12%
Basta aplicar os valores na fórmula para encontrar o retorno total:
Rp = (0,30 x 0,14) + (0,40 x 0,09) + (0,15 x 0,11) + (0,15 x 0,12)
Rp = 11,25%
Esse cálculo, embora simples, já demonstra uma característica essencial da teoria: a contribuição de cada ativo é proporcional ao seu peso, mas a análise ainda está incompleta, pois falta compreender como esses ativos interagem entre si no quesito risco.
Cálculo do risco da carteira
O risco é medido pelo desvio padrão, que expressa quão dispersos estão os retornos de um ativo em relação à sua média. Quanto mais volátil, maior o risco. Contudo, no contexto de uma carteira, o risco não é apenas a soma dos desvios padrão, e sim uma função que envolve também a relação entre os ativos.
É aqui que a fórmula se torna mais elaborada:
σp = √(wa² x σa²) + (wb² x σb²) + 2 x wa x wb x σa x σb x ρ(a,b)
Em que:
- σp é o risco total da carteira
- σa e σb são os desvios padrão
- ρ(a,b) é a correlação entre os ativos
Para ficar mais claro, imagine uma carteira de investimentos com dois ativos, X e Y, com pesos de 40% e 60%. A volatilidade dos ativos foi de 10% e 8%, respectivamente. Além disso, os ativos apresentam correlação de 0,45. Qual o risco esperado dessa carteira?
Calculando o risco da carteira
Para efetuar o cálculo basta substituir as letras da fórmula pelos valores correspondentes analisados na carteira. No entanto, sugiro que você dividida o cálculo em partes, para ficar ainda mais fácil.
σp = √ (0,40² x 0,10²) + (0,60² x 0,08²) + (2 x 0,40 x 0,60 x 0,10 x 0,08 x 0,45)
Viu como ficou muito mais simples do que parecia? Agora é só calcular passo a passo:
- σp = √ (0,16 x 0,01) + (0,36 x 0,0064) + (2 x 0,40 x 0,60 x 0,10 x 0,08 x 0,45)
- σp = √ 0,0016 + 0,0023 + 0,0017
- σp = √ 0,0056
Agora basta extrair a raiz quadrada:
σp = 0,074
Em seguida para transformar em porcentagem, multiplique por 100:
σp = 7,4%
Esse exemplo demonstra que a análise conjunta dos ativos altera substancialmente o risco final da carteira, e é exatamente por isso que portfólios diversificados podem ser mais seguros do que a simples soma de seus componentes.
A lógica da Fronteira Eficiente
A Fronteira Eficiente é o ponto crucial da Teoria de Markowitz, pois representa o conjunto de carteiras que oferece a melhor combinação de retorno e risco. Todas as carteiras abaixo dessa curva são consideradas subótimas, já que entregam menos retorno para o mesmo risco ou mais risco para o mesmo retorno.
A construção da fronteira se baseia em inúmeros cálculos de risco e retorno para diferentes combinações de ativos. Quando representados graficamente, os resultados formam uma curva semelhante a um projétil, conhecida como bullet.
Vamos entender na prática, imagine que de um lado você possui um ativo com risco zero, como o Tesouro Selic que hoje paga 13,25%, e de outro lado possui uma Ação com risco de moderado a alto, porém que tem um histórico de retorno de 18%.
Se você investir 100% do seu dinheiro em Tesouro Selic terá risco zero na carteira, mas seu retorno será quase 5% menor do que se investisse na Ação.
Da mesma forma, se investir 100% na Ação terá um retorno maior, mas com isso seu risco também aumentará consideravelmente.
Fronteira Eficiente para melhor distribuição
Qual a melhor distribuição de capital entre os dois ativos então para que você possa ter o maior retorno possível com o menor risco? É aí que entra a fronteira eficiente.
A Fronteira Eficiente é a linha em um gráfico que marca os pontos onde estão as melhores combinações de ativos na relação risco e retorno, em outras palavras, delimita onde está otimizada essa relação.
Abaixo está a construção de uma fronteira eficiente com carteiras hipotéticas:
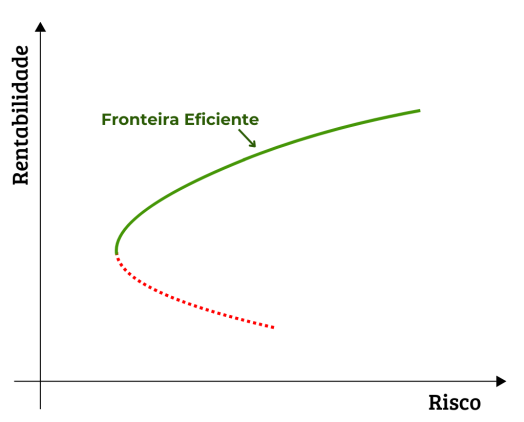
Cada um dos pontos na linha da Fronteira Eficiente representa uma carteira considerada eficiente, ou seja, não existe outra combinação para dado retorno e nível de risco que seja superior a observada.
Dessa forma, qualquer carteira que esteja abaixo da Fronteira Eficiente é considerada “inferior” a que está situada na fronteira, isso porque oferece um retorno menor para o mesmo nível de risco assumido
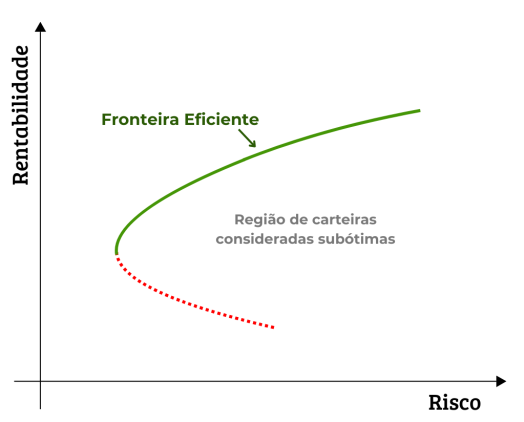
A interpretação é direta:
- carteiras na curva são eficientes
- carteiras abaixo da curva são inferiores
- não existem carteiras acima da curva
A partir desse ponto, o investidor já consegue identificar onde sua carteira está posicionada e quais ajustes podem aproximá-la do máximo de eficiência.
Fronteira eficiente e CML: o modelo com ativo livre de risco
Um dos desdobramentos da teoria é a Capital Market Line (CML), que surge ao se incluir no gráfico um ativo livre de risco, como títulos do Tesouro Nacional. A partir do ponto de risco zero e retorno do ativo livre de risco, traça-se uma reta crescente, indicando que, conforme o investidor aceita mais risco, deve ser compensado com maiores retornos.
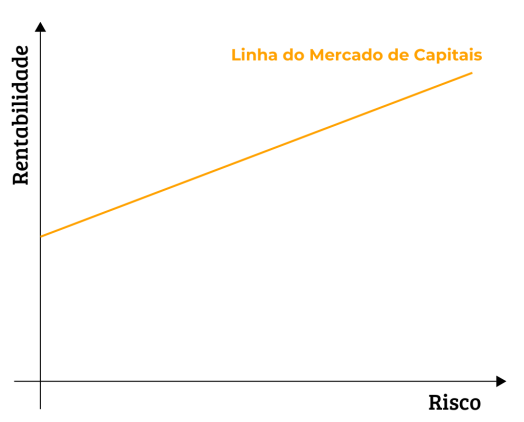
O ponto onde a CML toca a Fronteira Eficiente é chamado de carteira de mercado. Nesse ponto, o investidor tem acesso à melhor combinação possível entre ativos de risco. Qualquer alocação acima ou abaixo desse ponto representa carteiras ajustadas ao perfil do investidor, combinando diferentes proporções entre ativo livre de risco e carteira de mercado.
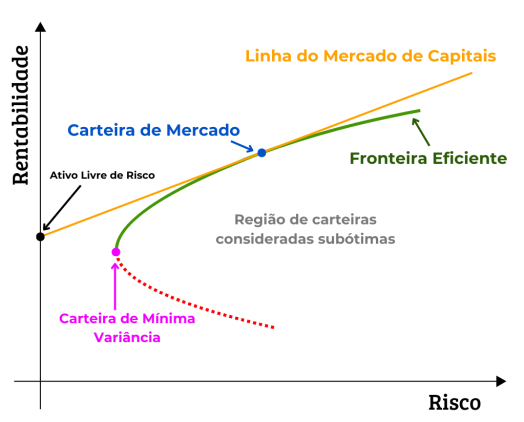
É nesse momento que muitos profissionais de investimentos utilizam o conceito para mensurar o retorno exigido, avaliar a eficiência de estratégias e analisar se um portfólio está realmente em linha com seu perfil e objetivos.
Vantagens da Teoria de Markowitz
Entre as principais contribuições do modelo, destacam-se:
- padronização da análise de risco e retorno
- base matemática para decisões de alocação
- uso da diversificação como ferramenta estruturada e mensurável
- clareza na construção de carteiras eficientes
- possibilidade de personalização das carteiras por perfil de risco
Na prática, a teoria ajuda a entender por que uma carteira com ativos menos arriscados pode, em determinados casos, entregar um retorno ajustado ao risco superior ao de carteiras agressivas mal diversificadas.
Limitações do modelo
Apesar de robusta, a teoria apresenta algumas limitações. O modelo parte do pressuposto de que os retornos seguem uma distribuição estatística estável ao longo do tempo, o que nem sempre ocorre em mercados emergentes como o Brasil, onde choques macroeconômicos podem alterar drasticamente o comportamento dos ativos.
Além disso, a correlação entre ativos não permanece constante. Em momentos de crise, por exemplo, é comum observar correlações aumentarem, reduzindo a eficácia da diversificação.
Ainda assim, mesmo com suas restrições, o modelo de Markowitz permanece como a base da engenharia quantitativa aplicada a investimentos. Ele fornece a estrutura inicial sobre a qual ferramentas modernas como CAPM, Black-Litterman e abordagens multifatoriais foram desenvolvidas.
A Teoria de Markowitz e o caminho para o valuation profissional
A compreensão da relação entre risco e retorno não serve apenas para montar carteiras. Ela é também o ponto de partida para análises mais profundas de precificação de ativos, inclinação da curva de risco e determinação de taxa de desconto em modelos de valuation.
Se você deseja compreender como esses conceitos se conectam ao cálculo de valor intrínseco de uma empresa, aconselho que leia o guia completo Como calcular o preço justo de uma ação (Valuation), que aprofunda a construção da taxa de desconto e a interpretação financeira dessa lógica dentro da análise fundamentalista.
Conclusão
A Teoria de Markowitz permanece como uma das estruturas mais elegantes e influentes da análise moderna de investimentos. Ao organizar risco e retorno de forma matemática, ela oferece ao investidor uma forma objetiva de decidir, comparar e otimizar portfólios em diferentes cenários. Mais do que um modelo estatístico, trata-se de uma metodologia que ajuda a enxergar a carteira como um organismo vivo, onde cada ativo influencia o conjunto.
No mercado brasileiro, em que oscilações econômicas podem alterar preços rapidamente, utilizar a lógica de diversificação eficiente não é apenas uma escolha técnica, mas uma necessidade estratégica. Compreender a fronteira eficiente e a relação entre risco e retorno torna qualquer investidor capaz de avaliar suas decisões com mais clareza.
Aprofundar-se nesse tipo de conhecimento é o que abre portas para modelos mais avançados de análise e para uma compreensão superior da precificação de ativos. Se você deseja evoluir no universo dos investimentos, continue estudando, conectando conceitos e explorando modelos que tragam profundidade às suas decisões financeiras.